De reeksen die ontstaan door de voorgaande waarde steeds met de zelfde waarde te vermenigvuldigen ben je al tegen gekomen op de pagina's "Basis uitleg 1 en 2". De figuren die ontstaan door deze reeksen te bewerken met een modulo bewerking zijn iets complexer dan de figuren die ontstaan met herhaald optellen, maar zijn in wezen toch simpel. Zoals op de pagina "Basis uitleg 2" te zien is kun je deze figuren bewerken met een interferentiepatroon. De mogelijkheden zijn echter beperkt als je dit vergelijkt met de mogelijkheden van de reeks van Fibonacci. Onderstaande zijn enkele basispatronen weergegeven die met deze reeksen gevormd kunnen worden.

Ook de reeksen die ontstaan door herhaald vermenigvuldigen zijn weer te geven als een Vedisch vierkant. In onderstaande Excel voorbeeld bestaan de X en Y as uit getallen die ontstaan zijn door herhaald vermenigvuldigen met 11en daarna bewerken met modulo 29. De getallen in het vierkant zijn berekend met de formule (X * Y) modulo 11. De figuur onder het Excel voorbeeld geeft de oppervlakte grafiek weer van dit getallen vierkant.

Onderstaande nog enkele andere voorbeelden.

Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 5

Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 6

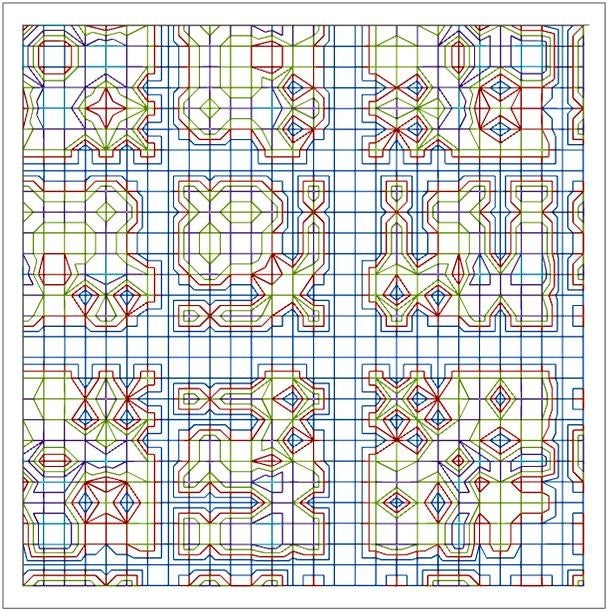
Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 7

Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 8

Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 9

Herhaald vermenigvuldigen met 11 modulo 29, (X * Y) modulo 10