Interfereren wil zeggen op elkaar inwerken. Het begrip interferentiepatroon wordt doorgaans gebruikt voor het patroon dat ontstaat als twee of meer golfpatronen met elkaar interfereren. Ik gebruik het begrip voor ieder patroon waarmee ik interfereer. De basis en het resultaat is steeds een figuur. In onderstaande voorbeeld wordt voor de X as de kolom A als interferentiepatroon gebruikt en voor de Y as kolom B. Dit beïnvloeden gebeurd simpel door de waarden in de kolom X te vermenigvuldigen met de waarden in de kolom A, en de waarden in de kolom Y te vermenigvuldigen met de waarden in de kolom B waardoor de kolommen X2 en Y2 ontstaan. Het effect dat ontstaat is afhankelijk van hoe de frequentie van het interferentiepatroon zich verhoud tot de frequentie van het basispatroon, en hoe de opbouw van het interferentiepatroon is. In het onderstaande voorbeeld is de frequentie van het interferentiepatroon de helft van de frequentie van het basispatroon. Dit zorgt er voor dat de basisfiguur vervormt wordt maar nog steeds uit 4 punten bestaat die een symmetrisch figuur vormen.

In onderstaande voorbeeld is de frequentie verhouding tussen het basispatroon en het interferentiepatroon gelijk aan 4 : 3. De opbouw van het interferentiepatroon is vergelijkbaar met het vorige voorbeeld. Doordat het interferentiepatroon geen harmonische is van het basispatroon wordt het aantal punten vergroot. Het aantal punten wordt gelijk aan 12, dit is de kleinste gemene veelvoud van beide frequenties. Het figuur dat nu ontstaan is, is een uitgebreide versie van het basispatroon.

Het onderstaande voorbeeld is het zelfde als voorgaande maar nu met kleinere stappen van het interferentiepatroon. Door variaties te maken met de frequentie verhoudingen en de stapgrootte kun je een grootte variatie aan figuren creëren.

Door interferentiepatronen met een logaritmische verloop te gebruiken ontstaan er figuren met een optimale verdeling van punten en lijnen.

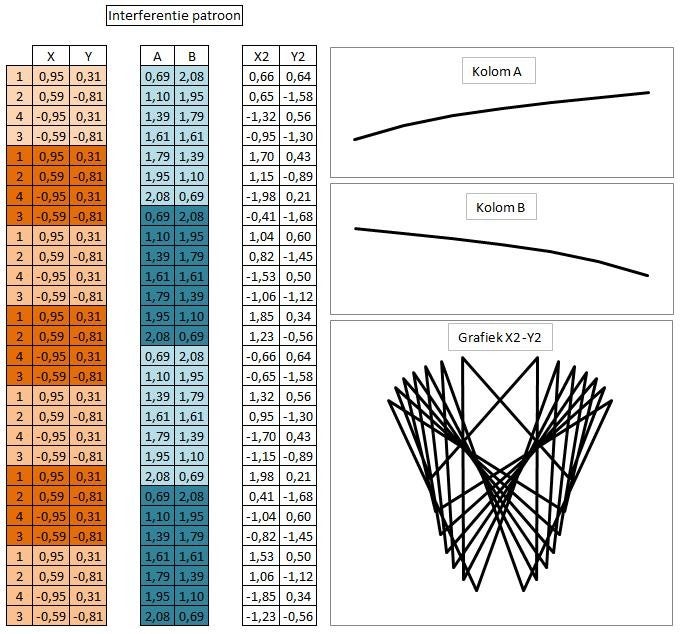
Alle bovenstaande voorbeelden zijn gebaseerd op de reeks die ontstaat na het vermenigvuldigen met 2 en daarna bewerken met modulo 5. Ik heb voor deze reeks gekozen omdat het de meest eenvoudig reeks is om iets uit te leggen. De mooiste figuren ontstaan echter uit de reeks van Fibonacci. Ook de keuze voor een logaritmisch interferentiepatroon in de uitleg is gedaan voor de eenvoud. Er bestaan namelijk vergelijkbare patronen die nog mooiere plaatjes produceren. Mijn voorkeur gaat uit naar interferentiepatronen die gegenereerd kunnen worden met de superformule van Johan Gieles of met de formule voor de Lorentz-factor. Het wonderlijke is dat beide formules op een bepaalde manier gebruikt ongeveer de zelfde getallenreeks produceren zoals hieronder te zien is.