Zelforganisatie is het proces waarbij in een chaotisch systeem spontaan structuren ontstaan. Bij elk chaotisch systeem waar een kracht aan toegevoegd wordt, bijvoorbeeld straling van licht of geluid, ontstaat er in grotere of kleinere mate een zelforganisatie. Deze structuren kunnen een steeds complexere vorm aannemen. Het ontstaan van structuren op kwantum-, atomair en moleculair niveau wordt mogelijk gemaakt door de werking van de natuurwetten.
Een belangrijk kenmerk van zelforganisatie is dat niemand doelbewust structuren in een systeem aanbrengt. Iemand kan natuurlijk wel voor de voorwaarden zorgen waardoor zelforganisatie kan plaatsvinden. Pure zelforganisatie is echter een theoretisch begrip. Het kan alleen plaatsvinden als er op een specifieke manier energie aan een systeem wordt toegevoegd. De entropie van een ongeorganiseerd systeem is immers hoger dan van een georganiseerd systeem.
Veel van de zelforganisatie in de natuur hangt samen met de harmonische reeks, de gulden snede , de rij van Fibonacci en de formules van Gödel en aanverwante reeksen. Volgens sommige wetenschappers is het leven ontstaan door zelforganisatie.
Het doel van mijn website is te laten zien dat het mogelijk is dat vormen in de schepping spontaan kunnen ontstaan door recursieve processen. Een van de eenvoudigste en krachtigste voorbeelden van een recursief proces is de rij van Fibonacci. De rij van Fibonacci zoals wij die kennen divergeert uiteindelijk naar oneindig. Zodra je deze rij echter met behulp van modulo rekenen in een cirkelvormig proces verandert ontstaan meteen de twee meest belangrijke eigenschappen van de natuur en wel symmetrie en herhaling. Een groot gedeelte van de voorbeelden op mijn website is dan ook gebaseerd op de rij van Fibonacci.
______________________________________________________________________________________________________________
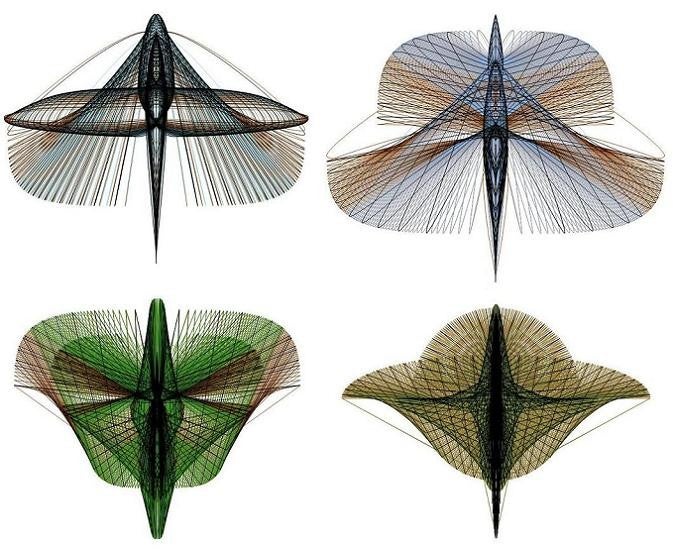
Onderstaande ziet U enkele voorbeelden van Fibonacci Super Lissajous figuren.
Deze vormen zijn ontstaan door relatief eenvoudige bewerkingen van de reeks van Fibonacci.
zie voor het zelf creëren van onderstaande objecten de pagina’s “De Bloem”, “De Libelle” en “Technische uitleg”
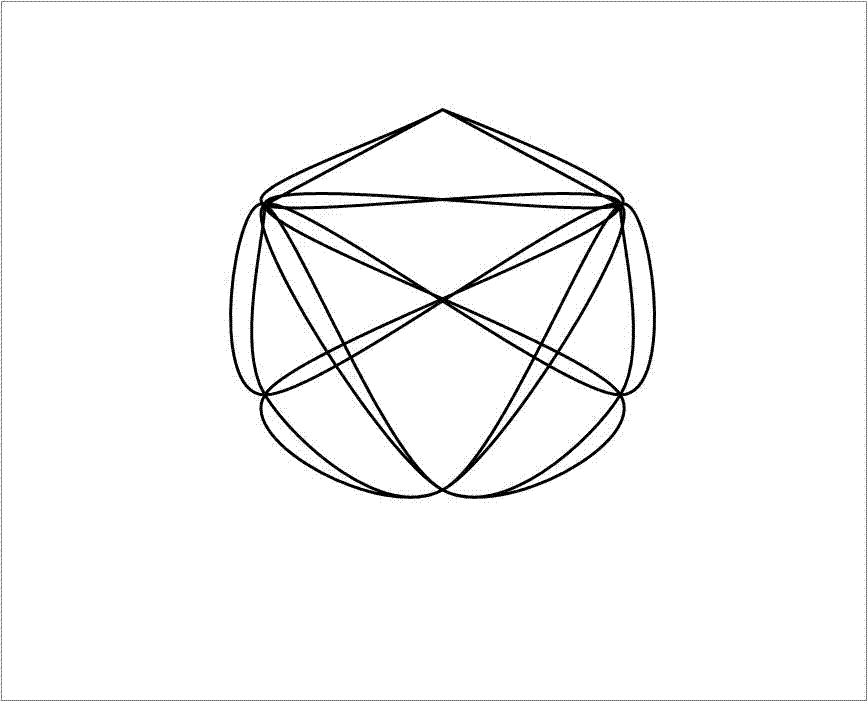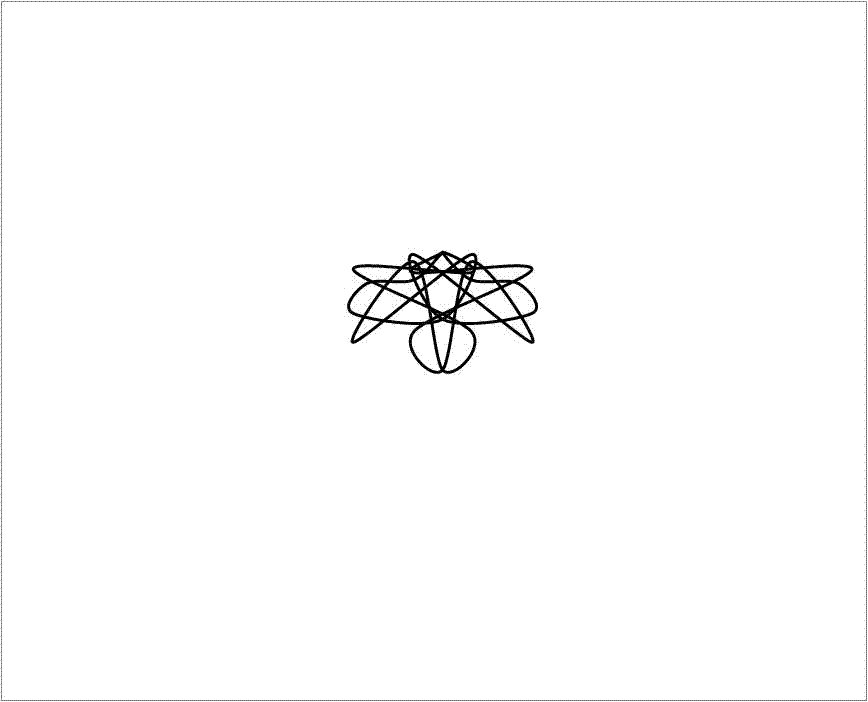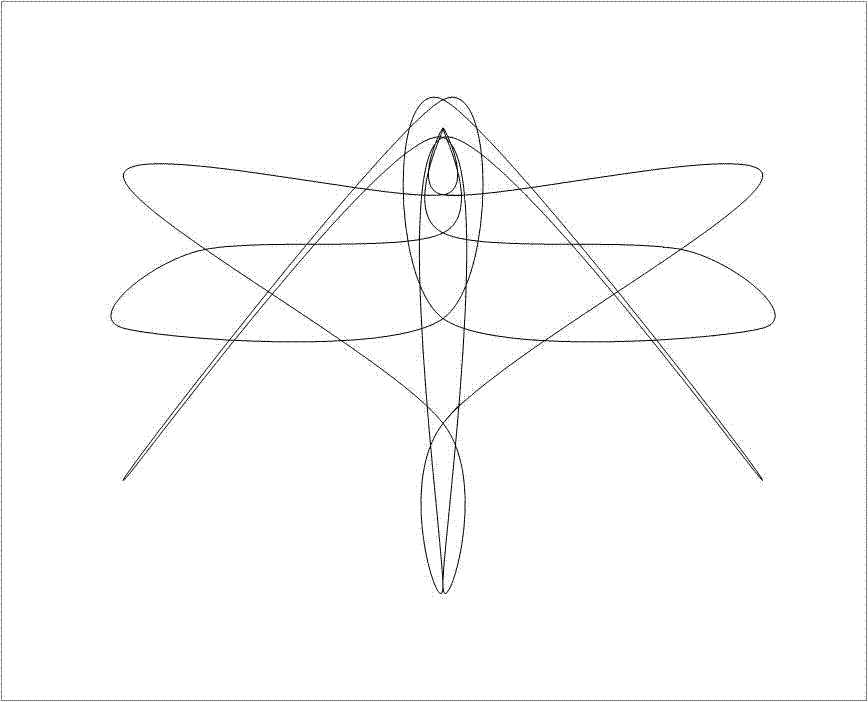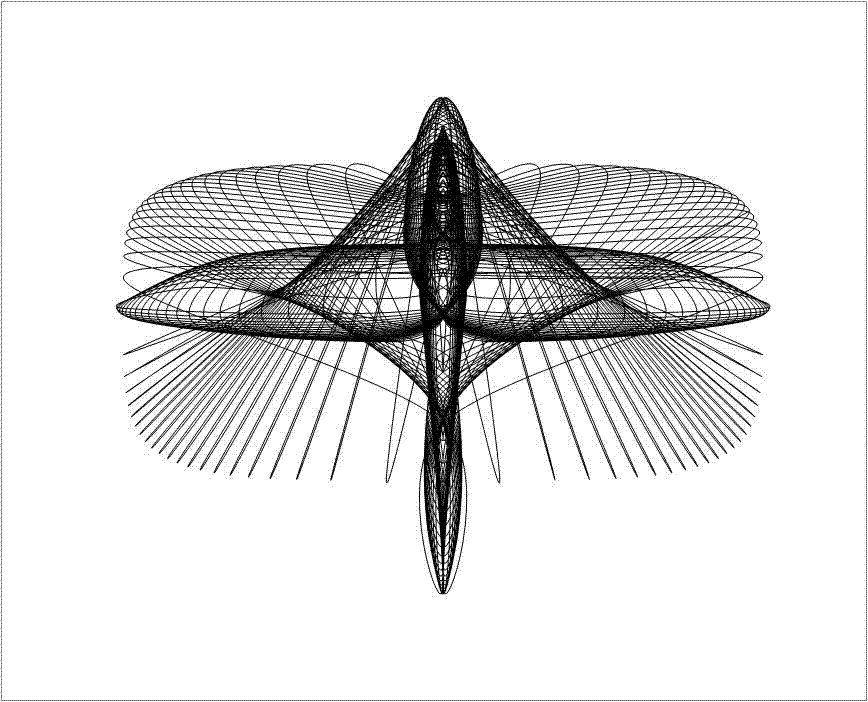
Onderstaande animatie laat zien hoe een eenvoudige embryonale vorm zich kan ontplooien tot een Libelle.
Onderstaande afbeeldingen laten een alternatieve manier zien om Lissajous figuren weer te geven.
Zie voor uitleg de pagina Lissajous speciaal.


Onderstaande Fractal toont aan dat door herhaling van een relatief eenvoudige functie een zeer complex figuur kan ontstaan.
De Fracal is gemaakt met het Mira iteratief systeem. De punten worden geplaatst met onderstaande concept.
xn+1 = yn + F(xn)
yn+1 = -xn + F(xn+1)
De startwaarden zijn x = -11,644 en y = 0,562 aantal herhalingen = 20000


Maak jouw eigen website met JouwWeb