Deze uitleg is bedoeld voor diegenen die zelf met Excel aan de slag willen met mijn figuren en onvoldoende kennis hebben om zelf een start te maken. Enige vaardigheid met Excel is vereist omdat de meeste kleurenfiguren zijn opgebouwd met duizenden formules. Indien je niet in staat bent om formules snel te kopiëren in Excel ben je dagen met intypen bezig. De libelle op de homepage bestaat uit drie kleuren lagen. Voor de eenvoud beschrijf ik hieronder alleen de zwarte laag.

 Zoals in onderstaande schema te zien is gebeurd de opbouw in 3 fases

het begrip interferentiepatroon wordt doorgaans gebruikt voor het patroon dat ontstaat als twee of meer golfpatronen met elkaar interfereren.
Ik gebruik het begrip voor ieder patroon waarmee ik interfereer. De basis en het resultaat is steeds een figuur.

Fase 1

In de kolom B van onderstaande figuur wordt de reeks van Fibonacci modulo 6 gegenereerd. De waarden 1 en 5 in de blauwe cellen zijn de startwaarden. Deze startwaarde kun je later wijzigen zodat je andere figuren krijgt. De waarden die in de kolom B ontstaan worden in de kolommen C en D omgerekend naar Catresische coördinaten. Excel werkt niet met graden maar met radialen. Dit wil zeggen dat je in de formules graden om moet rekenen naar radialen. De formule is in wezen bijzonder simpel. Omdat je met modulo 6 werkt moet de omtrek van de cirkel in 6 stukken worden verdeeld, dit doe je door 360 te delen door 6. Daarna vermenigvuldig je met de waarde uit de Fibonacci reeks zodat je op de juiste plaats op de cirkel uitkomt. Met de Sinus bereken je de X as en met de Cosinus de Y as en klaar is Kees. Het enige wat je nog moet doen is de cellen C3 t/m D23 selecteren en deze weer te geven als een sprijdingsgrafiek. Je kunt bij spreidingsgrafieken kiezen uit rechte lijnen en gebogen lijnen. Als je voor gebogen lijnen kiest zoals die gebruikt zijn voor het bovenstaande plaatje van de libelle krijg je de basisvorm van Fase 1.

Voor het vervormen van de basisvorm breiden we het bovenstaande voorbeeld in Excel verder uit. In de kolommen F en G bouwen we een interferentiepatroon op zoals hieronder in de blauwe cellen te zien is. Het patroon wordt naar onder toe herhaald door het kopiëren van de bovenstaande cellen. De lengte van het herhalend patroon van Fibonacci is 24. Om in harmonie met dit patroon te blijven maken we het interferentiepatroon 12 lang. In de kolommen C en D worden de formules aangepast zodat de oude waarden vermenigvuldigd worden met de waarden van het interferentiepatroon. De spreidingsgrafiek van de cellen C3 t/m D27 laat nu de vervormde figuur zien uit Fase 2.

Het vervormen van het basispatroon is mogelijk met ieder interferentiepatroon dat een harmonische is van de frequentie van het basispatroon. De frequentie van het bovenstaande basispatroon is 24, de harmonische zijn dan 2, 3, 4, 6, 8 en 12. Hieronder zie je een tabel waarin ik een voorbeeld van iedere harmonische heb weergegeven. De getallen zijn voor de duidelijkheid opvolgend, maar dit is niet noodzakelijk.

Indien je in het voorgaande Excel model de waarden in de kolommen F en G vervangt door de waarden uit bovenstaande tabel, dan zullen de onderstaande figuren gevormd worden.

In bovenstaande voorbeelden is te zien dat interferentiepatroon 8 geen symmetrische figuur oplevert. Als je in de tabel kijkt wordt het je misschien duidelijk waarom dit zo is.

Het is ook mogelijk om meerdere interferentiepatronen tegelijk te gebruiken. Ieder patroon wordt dan een extra vermenigvuldigingsfactor in de formule, b.v. SIN(RADIALEN(360/6)*B3)*F3*I3*L3 enz.. De interferentiewaarden zijn dan F3, I3 en L3. In onderstaande voorbeeld zie je het interferentiepatroon dat ontstaat als je de patronen 3 en 4 uit bovenstaande tabel samenvoegt.

 In muzikale zin kun je zeggen dat je meerdere tonen samenvoegt tot een akkoord.

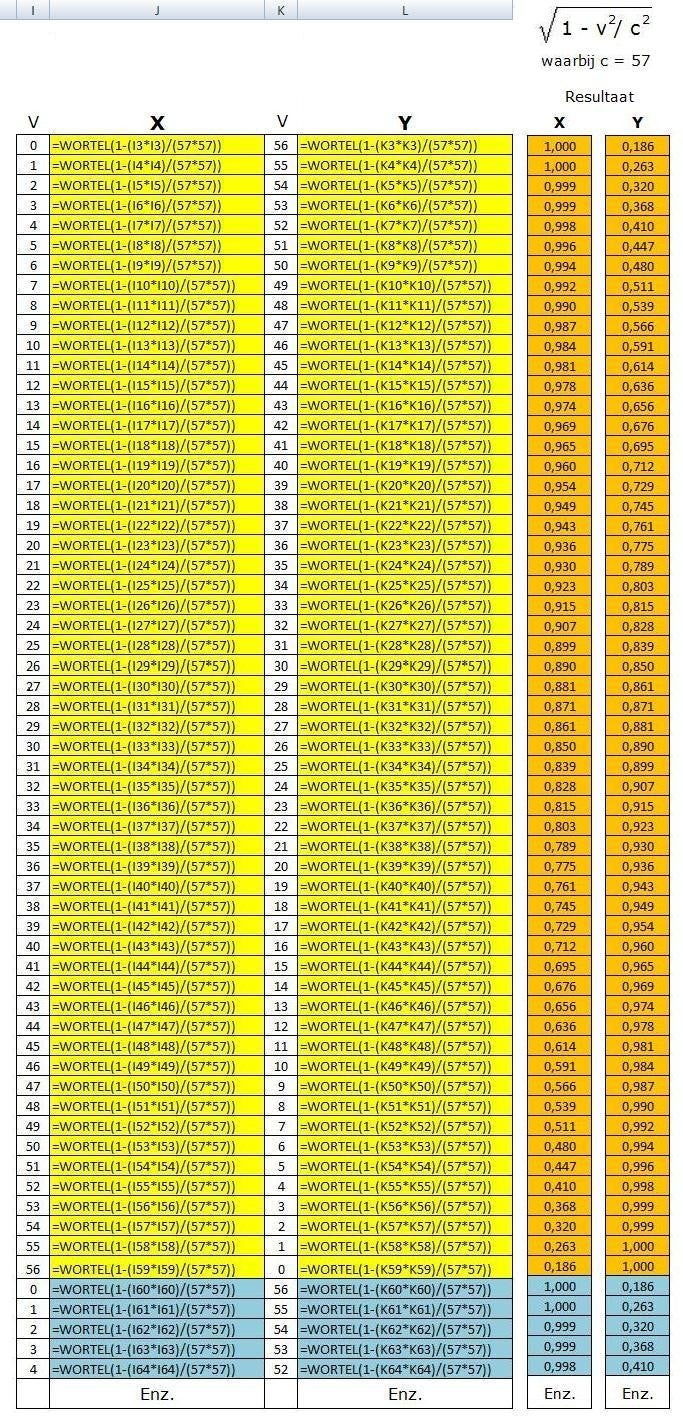
Met bovenstaande uitleg zijn we nu toe aan fase 3 van de libelle. In deze fase wordt gebruik gemaakt van niet harmonische interferentiepatronen. Het effect van een niet harmonisch interferentiepatroon is dat een figuur dat uit vorige bewerkingen is ontstaan volgens een bepaald patroon wordt vermeerderd. De figuur die ontstaat wordt getekend uit een lijn, maar is als het ware een trillingspatroon van het originele patroon. Het verloop van de getallen in het interferentiepatroon is volgens een bepaalde kromme. Bij de libelle maak ik gebruik van de kromme die ontstaat door de formule van de Lorentz transformatie te gebruiken. In onderstaande tabel is een gedeelte van het patroon weergegeven. Het patroon moet net zo lang herhaald worden tot het samenvalt met het basispatroon. Dit moment is gelijk aan de kleinste gemene veelvoud van de frequentie van het  basispatroon en de frequentie van het interferentiepatroon. Bij de libelle zijn deze frequenties 24 en 57.  Het totale patroon is dus 1368 regels lang.