Chaos, Fractals en Dynamische systemen

De chaostheorie is de populaire benaming voor het gebied binnen de wiskunde dat het gedrag van bepaalde systemen onderzoekt. De officiële naam binnen de wiskunde is dynamische systeemtheorie. Het onderzoekt de omstandigheden en eigenschappen van systemen waarbij deterministische chaos optreedt. Het begrip chaos heeft hierbij een technische betekenis en staat los van hetgeen er in het dagelijks gebruik mee bedoeld wordt. Deterministische chaos betekent dat de schijnbare wanorde toch exact bepaald is en geordend tot stand komt volgens een algoritme of rekenregel, bv. via een differentiaalvergelijking of een recursieve functie ontwikkeling. Het doel van de chaostheorie is de stabiliteit en betrouwbaarheid van systemen te onderzoeken. Het is echter niet mijn bedoeling om de chaostheorie uitgebreid te gaan behandelen. Mijn doelstelling is de mogelijkheden van Excel te laten zien voor wat betreft functie analyse bij recursieve functie ontwikkelingen en het creëren van Fractals. Een functie kun je zien als de wiskundige weergave van een actie in een proces waarbij een gegeven input omgezet wordt naar een bepaalde output. In een proces wordt een functie ook wel eens aangeduid als de afbeelding van een actie. In veel gevallen heeft een proces een recursief karakter. Een goed voorbeeld van zo’n proces is de groei van een populatie. In een wiskundig model voor de groei van een populatie maken we gebruik van een afbeelding die als input het bevolkingsaantal in een bepaald jaar heeft, en als output het aantal dat er volgens het model een jaar later zou moeten zijn. Door vervolgens die output weer als input te gebruiken, krijg je het aantal in het jaar daarna, enzovoorts. Op die manier produceert het model, uitgaande van een startwaarde voorspellingen voor de groei van een populatie in een hele reeks opvolgende jaren. Met de computer kan zo’n simulatie razend snel worden uitgevoerd, niet alleen voor één startwaarde, maar voor net zo veel starwaarden als je wilt. Zo ontstaat er inzicht in de eigenschappen van het model. Het eenvoudigste model voor de groei van een populatie is het model voor een ongeremde groei, wat er als volgt uit ziet: x_n+1 = ax_n  waarbij a de groeifactor voorstelt. In groeimodellen gaat men voor de waarde van x uit van de volgende aanname: 0 ≤ x ≤ 1. Waarmee je x dus kunt zien als een factor voor de werkelijke populatie. Indien je dit model in Excel weergeeft waarbij je uitgaat van a = 2 en de startwaarde van x = 0,01 krijg je onderstaande model.

In dit model is duidelijk te zien dat het proces al na 6 stappen een niet realistische waarde geeft. Van dit model heeft P.F. Verhulst in 1845 een wat meer realistisch model afgeleid met geremde groei, waarbij aangenomen wordt dat de factor afneemt naarmate de aantallen x toenemen. Het maximum dat het milieu toelaat is x = 1. Bij aanwezigheid van bv. x insecten is 1 – x een maat voor de vrije ruimte die in de natuur nog uitbreiding van de populatie toelaat. Het ligt dan voor de hand a te vervangen door a(1 – x). Het model wordt dan x_n+1 = ax_n(1 – x_n). Indien we dit model met de zelfde waarde als bovenstaande model in Excel weergeven zien we het onderstaande.

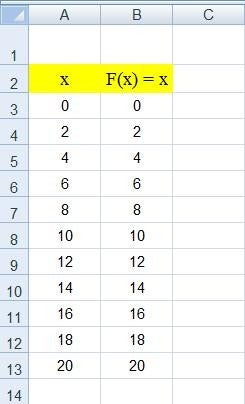
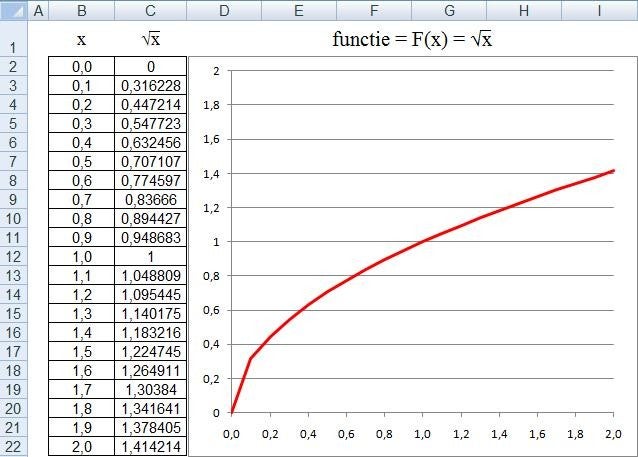
Om te begrijpen wat een functie doet kan men deze het beste weergeven in een grafiek. Een grafiek van een functie geeft in een heldere presentatie een afbeelding van al de waarden binnen het bereik van deze functie. De grafiek van de functie F is een deelverzameling van het Cartesische vlak (het xy-vlak), namelijk de deelverzameling bestaande uit alle punten van de vorm (x,F(x)). Dat wil zeggen: voor elke toelaatbare waarde van x wordt de input-waarde x gecombineerd met de output-waarde F(x) om het punt (x,F(x)) van het xy-vlak te vormen. Als bijvoorbeeld F(x) = x, dan is de grafiek van F de deelverzameling bestaande uit de punten (x,x). In dit geval bestaat de grafiek dus uit die punten van het xy-vlak, waarvan de x- en de y-coördinaat aan elkaar gelijk zijn. We hebben dus te doen met de rechte lijn die een hoek van 45° maakt met de x-as en met de y-as zoals in onderstaande figuur te zien is.

Het construeren van zo’n grafiek is met Excel een fluitje van een cent. Maak eerst een kolom met alle waarden in het bereik en maak een tweede kolom waar alle punten (x,F(x)) worden berekent. Selecteer beide kolommen en maak een spreidingsgrafiek met rechte lijnen. Een spreidingsgrafiek is de Excel benaming voor een xy-grafiek. Onderstaande de kolommen voor de functie F(x) = x. 

Iedere functie is op deze manier weer te geven.
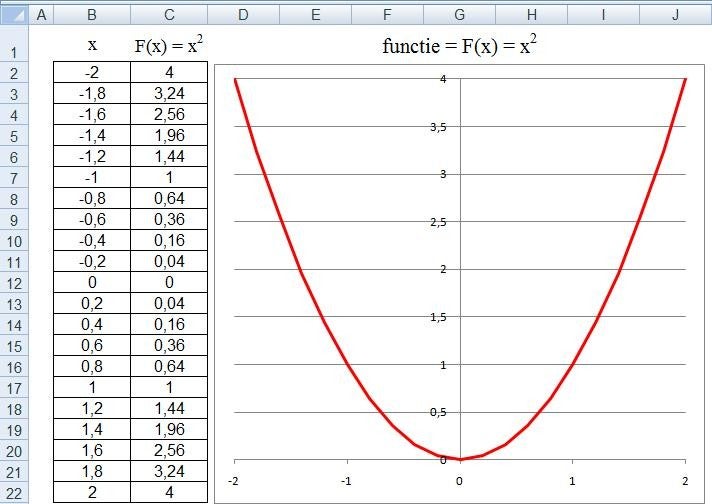
Enkele bekende functies die je in één oogopslag moet kunnen herkennen zie je hieronder weergeven.

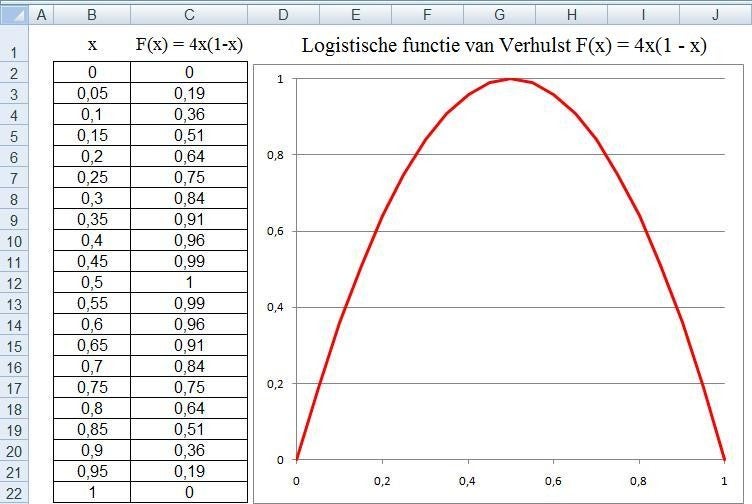
Enkele Voorbeeld van Mira fractals